There is a question I’ve been asking myself a lot since I’ve started the process of editing my draft. There are no questions about the fact that any suggestion I manage to blend with the story makes it better, this is the point in showing the story to someone who hasn’t been working on it an can give objective feedback.
But the question is still there: how good is good enough? Is there a threshold separating a good story from a bad one? A threshold above which the story becomes “perfect”? What happens if I keep moving forward after I reach perfection? Do I stop progressing or does it take me back to a less than perfect result?
The funniest part about this is that all those questions bring back my dormant math and science background because I’ve realized that I am looking at perfection as if it was a function of some variable, with its peaks, valleys, and asymptotes.
Some functions have bounded codomain, meaning that they can never get above and below a certain value. Some others have only an upper bound or a lower bound, some of them have none and can go to infinity. What kind of functions is perfection?
If we consider perfection to be universal and absolute, it has to be a monotone increasing function, meaning that its output can never decrease. It leaves us with two possibilities: the function has an upper bound, or it doesn’t and it can go to infinity. I think both cases could be used to describe perfection, but the way I think about it is the following one: an upper horizontal asymptote.
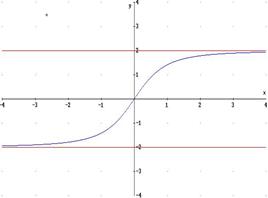
Perfection is the upper red line, of course, and the black one is how we approach it. At first, we have no direction and therefore we don’t know how to improve our work, then something clicks and we quickly improve. After a while, improving more becomes harder and harder, but not because we’re unable to: because we’re already very good and each modification is a small tweak rather than a complete revolution. Note that it would be the same if the function had no upper bound and went to infinity, but I liked it more to have a clear and visible limit for the function.
In this sense, we’ll never reach perfection, because the black curve never touches the red line. It gets closer and closer, but it never reaches it. Is that a bad thing in itself? I think it’s not. Even if it’s not perfect, it’s close enough, and the only thing to figure out when to stop with the optimization. The answer depends on us I think, on how much we’re willing to lose our sleep on improving something already good.
This seems like an easy solution, and also a quite fortunate case. What if it was possible to actually make your work worse with too much optimization? I’m thinking about a not monotone function like this one:
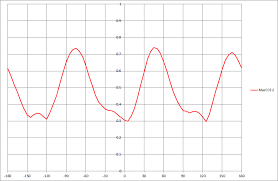
I think that if that’s the case, then we’ve got even less to worry about: if you remember, as conditions for the monotone increasing function we had that perfection had to be universal and absolute, i.e. it’s measurable and everybody agrees upon it. It means that we know what we have to do to improve and that the result is guaranteed to be better.
The second figure, to me, looks like a situation where there is no agreement on the concept of perfection. I can give you my two cents about how to make something better, but it doesn’t mean everyone will agree with me: the end result could be considered worse than it was before.
As I said, in this case, we should not worry about it: aside from the basic rules of the craft, it becomes a matter of preference, and we already know we can’t please everyone. The rules of the craft are the part that can be optimized (monotone function), the personal preference is the part with peaks and valleys. In both cases, there’s no way to reach perfection, and in both cases, it’s up to us to decide when to stop.
I don’t know about you, but I love to have all this power in my hands.
Be First to Comment